lotuskerop.blogg.se - Half adder truth table to circuit

Now, let us understand the logic behind how the addition of 1 and 1 will generate 0 as the sum and 1 as the carry.

1 + 1: When the half adder adds 1 with 1 then it produces 0 as the sum and 1 as the carry.

1 + 0: Like in the previously discussed case here also the addition of 1 and 0 will give 1 as the sum and 0 as the carry for the respective addition.

Whereas as no carry is generated thus carry bit will be 0.

0 + 1: The addition of 0 and 1 generates 1 as the output which is represented by the sum bit in the above table.

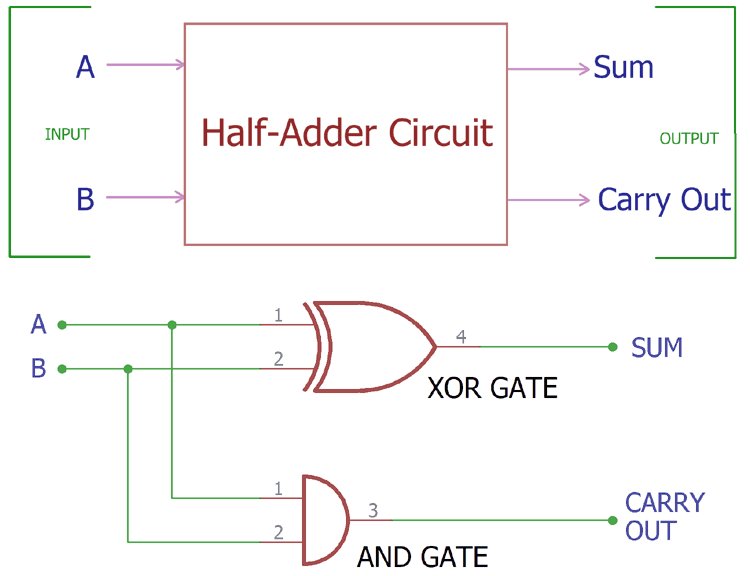
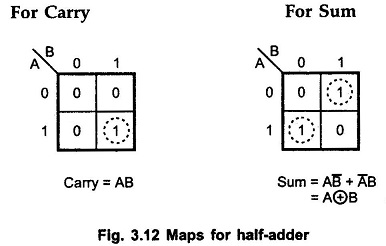
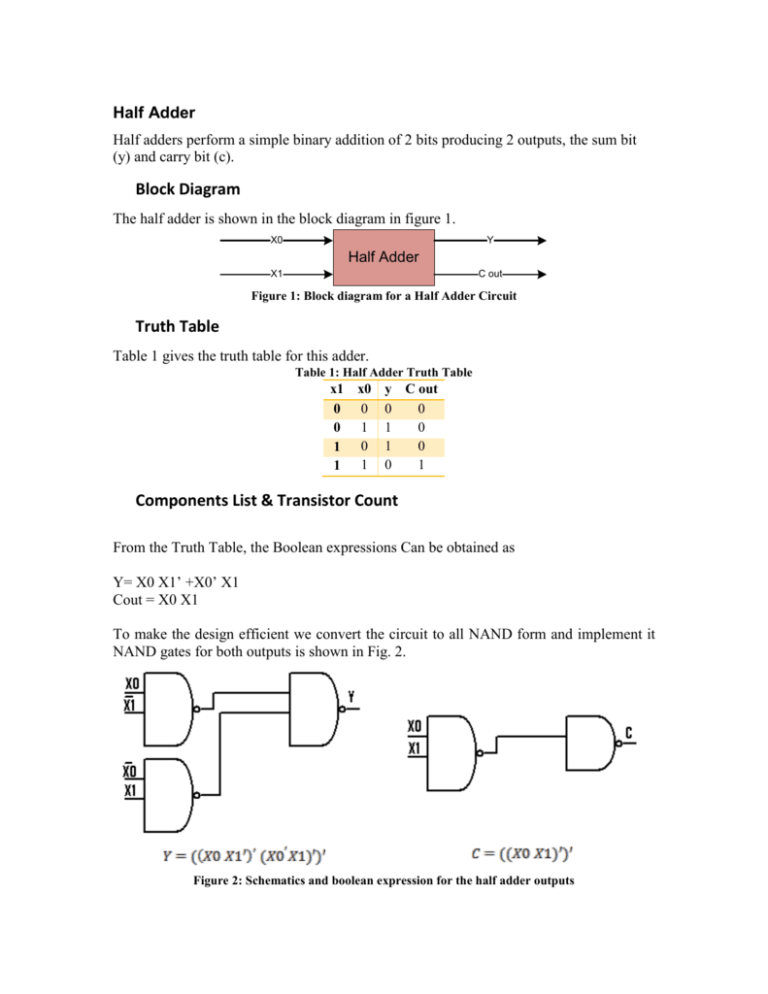
So, in this particular case, the bits representing the sum and carry both will be 0. 0 + 0: We know the binary addition of low and low i.,e 0 and 0 will give 0 as the output without generating a carry.Here, X and Y are the two, 1-bit binary numbers applied at the input of the half adder while S and C denote the sum and carry bits respectively. So, let us now consider the truth table for half adder showing binary addition of 1-bit numbers: However, the half adder operates on only a single bit. But in decimal as well as binary addition we have considered more than 1-bit number. In the previous section of this article, we have discussed, how the addition of decimal and binary numbers take place. We will discuss later how the addition of 1 and 1, provide 0 as the sum and 1 as the carry. But when the addition of 1 and 1 is performed then it will produce 0 as the sum and carry bit 1 will be generated. Further when the next bit is considered the summation of 1 and 0 will give 1 as the output. Let us now consider two binary values in order to understand the binary addition.Īs we can see the addition of 0 and 0 generates 0 as the sum. So, when the summation of the most significant column is considered then carry from the previous addition is considered. But while writing the result we simply write the LSB of the summation as the least significant bit of the output and the MSB acts as the carry bit. So, 6 is added with 5 and this summation generates 11 as its output. Here, we can see that we have started the addition with the least significant column. Then we will move further towards the addition of binary values. Let us take an example to understand how the addition of decimal number takes place. This is the way to perform basic addition. However, we have recently discussed that half adder performs the addition of only single bit numbers.Īt the time of addition of two-bits in case, a carry bit is generated then it gets added with the next column bit that is to be considered. This we have already discussed in half subtractor.Īlways the addition of two numbers begins with the least significant column and ends with the most significant column.

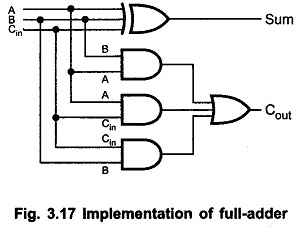
When subtraction of two numbers is performed then basically difference and borrow are the terms that are needed to be considered. And we all know the basic method used for adding two numbers. We know that adding two numbers will generate the summation of the two as a result.

It is noteworthy that, not all summations bring a carry with it, however, if it holds a carry then the carry bit is represented as high otherwise low. In simple words, we can say, that it adds two binary numbers of 1 bit each and generates the output as the sum and carry.